 Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una velocidad no nula, entonces la trayectoria de caída no es una recta sino una curva aproximadamente parabólica. La ecuación de la trayectoria en coordenadas cartesianas viene dada por:
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una velocidad no nula, entonces la trayectoria de caída no es una recta sino una curva aproximadamente parabólica. La ecuación de la trayectoria en coordenadas cartesianas viene dada por:(4)
La expresión de la velocidad vertical debe reescribirse en función de la coordenada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:
- Para un cuerpo en caída libre sin rozamiento, la trayectoria es exactamente una parábola dada por:
- Cuando se incluye el rozamiento aerodinámico, la trayectoria no es exactamente una parábola. Por ejemplo para una fuerza de rozamiento proporcional a la velocidad como en la () la trayectoria resulta ser:
Para una fuerza de rozamiento proporcional al cuadrado de la velocidad, la integración de las ecuaciones del movimiento es más compleja, presuponiendo fuerzas de rozamiento independientes en dirección horizontal y vertical proporcionales al cuadrado del valor de la componente:
La trayectoria viene dada por:
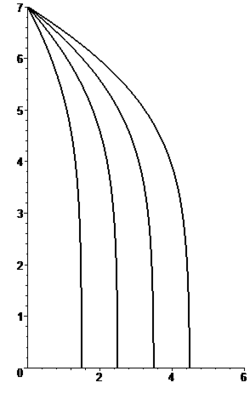
Las figuras adjuntas muestran la forma de las trayectorias para cinco valores diferentes del parámetro β para una misma altura de caída (medida en unidades de longitud δ).

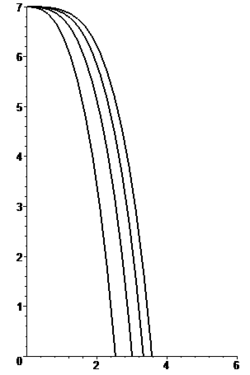

![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right] \qquad \begin{cases} \delta = gm^2/k_w^2\\ \beta = V_xk_w/mg\end{cases}](http://upload.wikimedia.org/math/2/4/9/2499cfce560492266eba090a5e021837.png)

![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right] \qquad \begin{cases} \delta = 1/C_w\\ \beta = \sqrt{g/(C_wV_x^2)} \end{cases}](http://upload.wikimedia.org/math/3/b/f/3bf3fe9845c590f97bd6f85495e3efd4.png)
hola q hace
ResponderEliminarhola guapo
Eliminarsexo¿
ResponderEliminar